Topological Manifolds
Definition 1. A topological manifold $M$ of dimension $n$ is a second-countable Hausdorff space which is locally Euclidean of dimension $n$.
“Locally Euclidean” means that for each $p\in M$, we can find an open subset $U$ such that $p\in U\subset M$ and a homeomorphism $\phi$ from $U$ to $\tilde{U} \subset \mathbb{R}^n$ (or $\mathbb{H}^n$, which means there is a boundary). Such $(\phi, U)$ is called a coordinate chart for $M$ at $p$. If $\tilde{U}$ is a ball, $U$ is called a coordinate ball. If in addition $\bar{U} \subset U’$ and $\phi$ can be extended to $U’$ such that $\phi(\bar{U})$ and $\phi(U’)$ are also balls, then $U$ is called a regular coordinate ball. A union of charts which is also a open cover of $M$ is called an atlas.
Proposition 1. Every topological manifold has a basis of regular coordinate balls.
Lemma 1 (Closed Map Lemma). If $X,Y$ are two topological space, $X$ is compact, $Y$ is Hausdorff. Then if $f: X\rightarrow Y$ is continuous, $f$ is a closed map.
Lemma 2. Let $M$ be a $n$-manifold. If $B’$ is a coordinate ball and $\phi: B’ \rightarrow B _{r’}$ is its coordinate map, then $\forall r< r’$, $\phi^{-1}(B _{r})$ is a regular coordinate ball.
Proof. Let $B = \phi^{-1}(B_r)$. We only need to prove that $\phi(\overline{B}) = \overline{B_r}$, or $\phi^{-1}(\overline{B_r}) = \overline{B}$. According to the closed map lemma, $\phi^{-1}$ is a closed map. So $\phi^{-1}(\overline{B_r})$ is a closed set. Since for any continuous map $f$, $f(\overline{A})\subset \overline{f(A)}$, so $B \subset \phi^{-1}(\overline{B_r}) \subset \overline{B}$. This means $\phi^{-1}(\overline{B_r}) = \overline{B}$.
Proof of Proposition 1. Take a countable basis $\mathcal{B’}$ of $M$. Define $\mathcal{\tilde{B}} = \cup_x B _{x, r(x)}$, where $x$ ranges over all points of $M$, $B _{x, r(x)}$ is a coordinate ball center at $x$ with radius $r(x)$ and is contained in some $B’\in \mathcal{B’}$. Let $\mathcal{B}=\cup _{x, r<r(x)}B _{x, r}$ where $x$ has rational coordinate, and $r$ is a rational. According to lemma 2, $\mathcal{B}$ is a basis of countable regular balls.
Corollary 1. Every topological manifold has a countable basis of precompact coordinate balls.
Corollary 2. Every topological manifold is locally compact, i.e. every point has a neighborhood contained in a compact subset.
Definition 2. $M$ is paracompact if every open cover admits an open, locally finite refinement.
Theorem 1. Given a topological manifold $M$, any open covers $\mathcal{X}$, and any basis $\mathcal{B}$, there exists a locally finite open refinement of $\mathcal{X}$ consisting of elements of $\mathcal{B}$. This means every topological manifold is paracompact.
Lemma 2. Every manifold $M$ admits an exhaustion of compact sets: $M = \cup_i K_i$, where all $K_i$ are compact and $K_i \subset K _{i+1}$.
Proof of theorem 1.
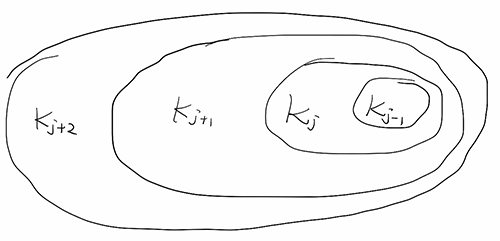 Take a compect exhaustion $M = \cup_i K_i$, define $V_j = K _{j+1} \setminus \text{Int}K _{j}$ and $W_j = \text{Int}K _{j+2} \setminus K _{j-1}$. So $V_j$ is compact, $W_j$ is open and $V_j \subset W_j$. For each $x\in V_j$, there is some $X_x \in \mathcal{X}$ such that $x\in X_x$, and there exists some $B_x \in \mathcal{B}$ such that $x\in B_x \subset X_x \cap W_j$. $O_j = \cup _{x\in V_j} B_x$ is an open cover of $V_j$, so has a finite subcover. $\mathcal{O} = \cup_j O_j$ is then a open refinement of $\mathcal{X}$. Since each $x\in M$ is contained in at most two $V_j$s, so $\mathcal{O}$ is locally finite.
Take a compect exhaustion $M = \cup_i K_i$, define $V_j = K _{j+1} \setminus \text{Int}K _{j}$ and $W_j = \text{Int}K _{j+2} \setminus K _{j-1}$. So $V_j$ is compact, $W_j$ is open and $V_j \subset W_j$. For each $x\in V_j$, there is some $X_x \in \mathcal{X}$ such that $x\in X_x$, and there exists some $B_x \in \mathcal{B}$ such that $x\in B_x \subset X_x \cap W_j$. $O_j = \cup _{x\in V_j} B_x$ is an open cover of $V_j$, so has a finite subcover. $\mathcal{O} = \cup_j O_j$ is then a open refinement of $\mathcal{X}$. Since each $x\in M$ is contained in at most two $V_j$s, so $\mathcal{O}$ is locally finite.
This theorem means that we can use any basis to refine any open cover to get a locally finite open cover.
Smooth Manifolds
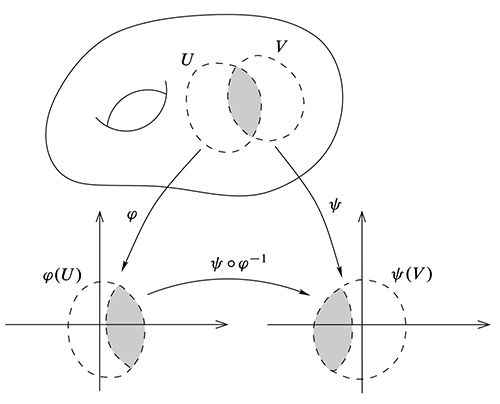 Definition 3. A manifold is smooth if it admits a smooth atlas.
Smooth altas means the transition map between any pair of charts $(U, \phi)$ and $(V, \psi)$: $\psi\circ\phi^{-1}$ is smooth from $\phi(U\cap V)$ to $\psi(U\cap V)$.
Definition 3. A manifold is smooth if it admits a smooth atlas.
Smooth altas means the transition map between any pair of charts $(U, \phi)$ and $(V, \psi)$: $\psi\circ\phi^{-1}$ is smooth from $\phi(U\cap V)$ to $\psi(U\cap V)$.
Given a smooth atlas $(U, \phi)$, we can continue to add charts such that the result is still smooth atlas (we just need to make sure that added chart is smooth compatiable with every charts which are in the atlas already) until we cannot find any such chart anymore. This altas is called a maximal smooth atlas or smooth structure.
Proposition 2. Every smooth chart $\mathcal{A}$ is contained in a unique smooth structure. Two smooth atlas determines the same smooth structure if and only if their union is still a smooth atlas.
Definition 4. Smoothness for boundary chart is defined as follows: For any pair of charts $(U, \phi)$ and $(V, \psi)$, where $U$ is a boundary chart (homeomorphic to $\mathbb{H}^n$), $\psi \circ \phi^{-1}$ can be extended to a smooth map on $\mathbb{R}^n$.
Reference
Introduction to Smooth Manifolds